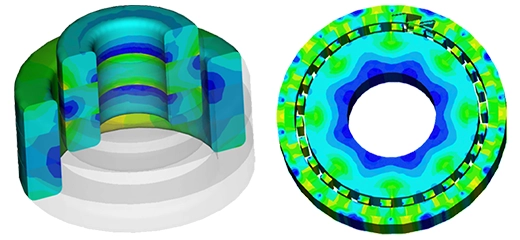
Multiphysics Simulation of Magnetorheological Elastomers
Magnetorheological elastomers
Magnetorheological elastomers (MREs) combine a polymer matrix with ferromagnetic particles, enabling adjustable mechanical properties via magnetic fields. Created by curing a mix of iron powder and silicone rubber, the alignment of iron particles during curing determines if the material is anisotropic or isotropic. MREs have revolutionized automotive suspension systems by allowing adjustable stiffness, reducing brake shuddering, and enhancing ride comfort through a control method that modulates stiffness with an electrical current in response to braking.
Example of industrial application of MRE's
The vibration isolator designed by Liao et al. [2] utilizes magnetorheological (MR) elastomers for adjustable stiffness and damping. It incorporates components like magnetic coils, a voice coil motor, and MR elastomer layers. The setup, with three coils generating magnetic fields for the elastomer layers, enables stiffness tuning, while the voice coil motor adjusts damping based on shear velocity. This design offers precise vibration isolation control.
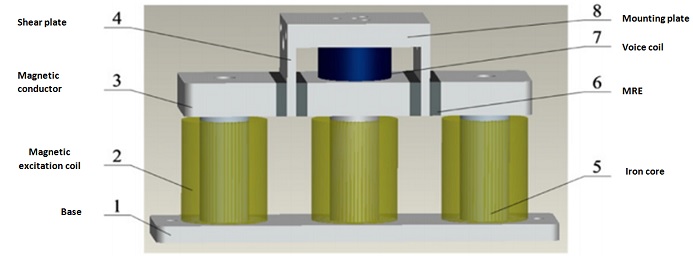
Figure 1 - Schematic of the MR elastomer-based vibration isolator designed by Liao and al.
CAD Model
The current study explores a model with a wound coil surrounding an elastomer, embedded with two ferromagnetic spheres. When an electrical current flows through the coil, it induces attractive forces between the spheres. This research aims to analyze the magnetic field's effect on the spheres. Traditional analytical methods simplify calculations by assuming a single force acting at each sphere's center of gravity, offering only approximate results. However, our numerical model achieves higher precision by calculating the forces at multiple points on the spheres, providing a detailed understanding of the magnetic interactions.
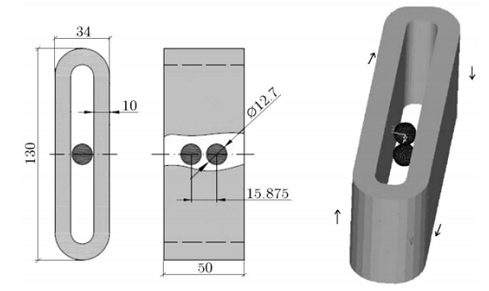
Figure 2 - Dimensions of the solenoid and spheres.
Multiphysics simulation using EMS
EMS software is key for integrating magneto-mechanical simulations, focusing on the effects of a magnetic field on ferromagnetic spheres. It sequentially analyzes magnetic forces, then calculates displacement and Von Mises stress based on these forces, offering a detailed insight into the interaction's mechanical impact.
Materials
Below in Table 1 are the properties of the used materials.
| Relative Permeability | Electrical Conductivity (Mho/m) | Elastic modulus (Pa) | Poisson's ratio | |
| Copper | 1 | 5.998e+07 | Not required | Not required |
| Steel | 10e+04 | Not required | 2e+11 | 0.3 |
| Elastomer | 0.99999 | 0 | 12e+04 | 0.45 |
| Air | 1 | 0 | Not required | Not required |
Electromagnetic inputs
A wound coil is specified as the current source for this problem, and its properties are detailed in Table 2 below.
Table 2 - The coil properties.
| Number of turns | Wire diameter (mm) | Current amplitude (A) | |
| Wound Coil 1 | 1 | 0.91168568 mm | 5000 |
Structural Inputs
Fixed constraint is applied on the following highlighted faces of the elastomer box, shown in Figure 3.
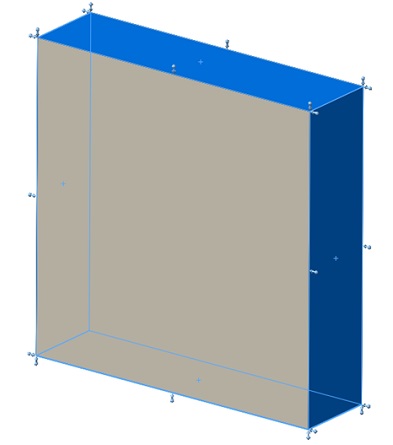
Figure 3 - Fixed constraint applied on the model faces.
Meshing
In Finite Element Analysis (FEA) models like EMS, the precision hinges on the mesh quality. EMS uses tetrahedral elements, allowing mesh refinement or coarsening to suit analysis requirements and model geometry. For ferromagnetic spheres, refining the mesh is vital for accurate magnetic force calculations and stress analysis, aiming to precisely determine the spheres' movement in a magnetic field.

Figure 4 - The steel spheres mesh.
Magneto-mechanical results
EMS offers the possibility of many types of plots. Below we can observe a fringe plot of the magnetic flux density.
Magnetic Flux density plot
Figure 5 shows the magnetic flux distribution in the elastomer pattern.
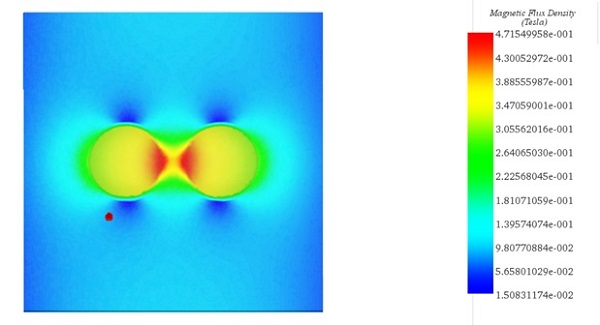
Figure 5 - Section clipping plot of magnetic flux density in the elastomer pattern.
Magnetic Force density plot
The magnetic force primarily focuses along the boundaries of ferromagnetic bodies due to the permeability difference between nonmagnetic and ferromagnetic materials, such as the elastomers and spheres. Known as Maxwell or reluctance forces, these forces cluster at interfaces with significant magnetic reluctivity changes, like the boundary between air and ferromagnetic material, leading to the attraction or repulsion seen between magnets.
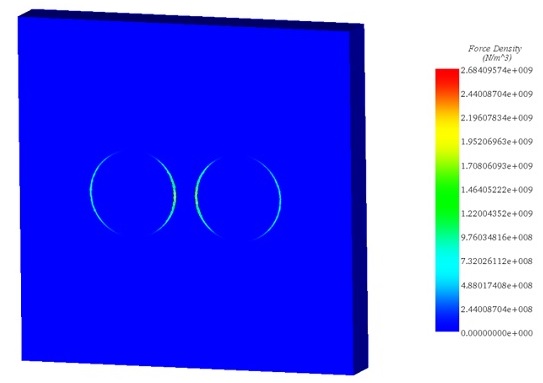
Figure 6 - Magnetic force density in the plane passing through the gravity center of the spheres.
Displacement plot
The elastomer pattern shows the highest deflection, as seen in Figure 7, with vectors indicating the ferromagnetic spheres are attracted towards each other by Maxwell forces, resulting in a maximum displacement of 0.11mm.
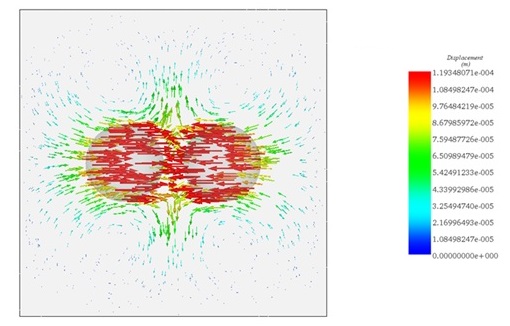
Figure 7 - Vector plot of displacement in the plane passing through the gravity center of the spheres.
Stress plot
The Von Mises stress plot, through the plane at the spheres' center of gravity, shown in Figure 8, indicates a mostly uniform stress within the elastomer, approximately 1.4 x 10^4 N/m^2 (Pa).
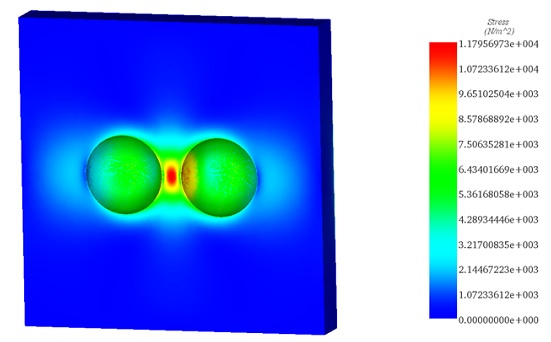
Figure 8 - Von Mises stress in the elastomer (section clipping is done by the plane passing through the gravity center of the spheres).
Conclusion
This application note explores the dynamic capabilities of magnetorheological elastomers (MREs), which blend a polymer matrix with ferromagnetic particles to create materials with magnetically adjustable mechanical properties. The study demonstrates how the alignment of iron particles within the elastomer—achieved through a curing process—determines the material's anisotropic or isotropic nature. A significant focus is placed on the innovative use of MREs in automotive suspension systems, highlighting their ability to adjust stiffness, reduce brake shuddering, and improve ride comfort through electrical current modulation in response to braking forces.
The note further delves into an industrial application example by Liao et al., showcasing a vibration isolator that employs MREs for tunable stiffness and damping. This isolator is designed to precisely control vibration isolation, featuring a combination of magnetic coils, a voice coil motor, and layers of MR elastomer to achieve stiffness and damping adjustments.
The study also introduces a CAD model involving a wound coil and ferromagnetic spheres within an elastomer, aiming to understand the magnetic field's impact on these spheres. Employing EMS software for magneto-mechanical simulations, the research provides insights into magnetic forces, displacement, and Von Mises stress, emphasizing the precision achievable through mesh refinement in Finite Element Analysis (FEA).
Key findings include the concentration of magnetic force along the boundaries of ferromagnetic bodies, maximum displacement observed within the elastomer pattern, and a uniform Von Mises stress distribution. These results underline the potential of MREs in various applications, from automotive engineering to vibration isolation technologies, showcasing the detailed analysis possible with advanced simulation tools.
References
[1]: A. Boczkowska, L. Czechowski, M. Jaroniek and T. Niezgoda.2010. Analysis of magnetic field effect on ferromagnetic spheres embedded in elastomer. Journal of theoretical and applied mechanics. Volume 48, issue 3, pp.659-676: Warsaw.
[2]: https://en.wikipedia.org/wiki/Magnetorheological_elastomer
[3]:Yancheng Li, Jianchun Li, Weihua Li and Haiping Du. Australia 2014. A state of the art review on Magnetorheological elastomer devices. Smart materials and structures. 23(12), pp.1-24.