Rechenkapazität eines Mehrstoffkondensators

Gebrauchte Werkzeuge:

Physik

Die Kapazität ist definiert als das Verhältnis der im Kondensator gespeicherten Ladungsmenge und der Potentialdifferenz zwischen den Elektroden.
Das Beispiel eines Parallelplattenkondensators in Abbildung 1 wird konstruiert, indem der Raum zwischen zwei quadratischen Platten mit Blöcken aus drei dielektrischen Materialien gefüllt wird.

Die Kapazität jedes dielektrischen Blocks ist durch die Gleichungen (1), (2) und (3) gegeben:

(Gl. 1)

( Gl. 2)
( Gl. 3)

, und sind die Dielektrizitätskonstanten einzelner dielektrischer Materialien, ist die Permittivität des freien Raumes, ist die Kondensatorplattenfläche und ist der Abstand zwischen den Platten. 1 zeigt, dass die Gesamtkapazität durch Verbinden einer Kapazität des dielektrischen Blocks gebildet wird parallel zu einer Reihenschaltung von Blöcken und . Daher ist die äquivalente Kapazität durch Gleichung (4) gegeben als:

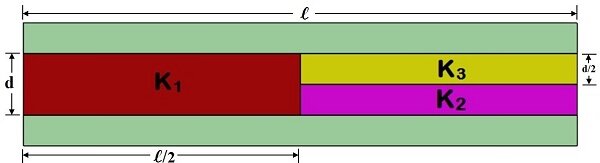
Abbildung 1 - Parallelplattenkondensator mit drei Dielektrika

Mit folgenden Parametern:



Die äquivalente Kapazität ist:

Modell

Die folgenden Anweisungen zeigen, wie Sie einzelnen Teilen Ihres Modells Material zuweisen und die Kapazität zwischen zwei Elementen berechnen.
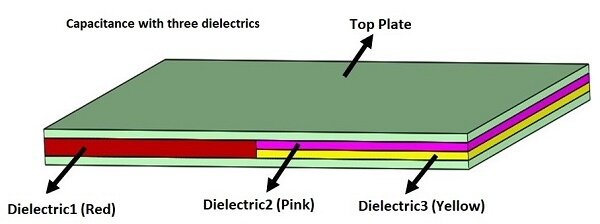
Das Modell des Kondensators mit Multipledielektrika wurde in Solidworks erstellt. Der Raum zwischen den parallelen Platten ist mit 3 verschiedenen dielektrischen Materialien gefüllt. Die Plattenoberfläche ist Die Dicke jeder Platte beträgt 1 mm. Dicke des dielektrischen Blocks entspricht dem Abstand zwischen den Platten: 2 mm; Dicke der Blöcke und ist die Hälfte davon: 1 mm (Abbildung 2).

Die Simulation wird in der Studie EMS Electrostatic durchgeführt . Aluminium wird als Material für die Elektrodenplatten verwendet, Teflon, Polyimid und Nylon werden als Dielektrikum verwendet , und , beziehungsweise. Alle diese Materialien mit ihren elektromagnetischen Eigenschaften finden Sie in der EMS-Materialbibliothek.

Material zuordnen

1. Klicken Sie im EMS-Manager-Baum unter Materialien mit der rechten Maustaste auf Dielektrikum 1.
2. Wählen Sie Material anwenden
3. Der Material Browser- Ordner wird angezeigt
4. Wählen Sie unter "Kabel" die Option "Teflon"
5. Klicken Sie auf Übernehmen und schließen

Kapazität berechnen

So erhalten Sie Kapazitätsergebnisse von EMS:

1. Klicken Sie im EMS-Krippenbaum mit der rechten Maustaste auf die elektrostatische Studie Mappe.
2. Wählen Sie Eigenschaften
3. Aktivieren Sie unter Allgemeine Eigenschaften das Kontrollkästchen Kapazität berechnen
4. OK klicken .

Randbedingungen

1. Klicken Sie in der EMS-Managerbaumstruktur mit der rechten Maustaste auf Laden/Zurückhalten Mappe.
2. Wählen Sie Floating Conductor .
3. Klicken Sie in die BodiesSelection Kästchen und wählen Sie dann die Deckplatte .
4. OK klicken .

1. Klicken Sie in der EMS-Managerbaumstruktur mit der rechten Maustaste auf Laden/Zurückhalten Mappe.
2. Wählen Sie Floating Conductor .
3. Klicken Sie in die BodiesSelection Feld und wählen Sie dann die Bodenplatte .
4. OK klicken .

Ergebnisse

In der EMS-Krippenstruktur unter Ergebnisse Öffnen Sie die Ergebnistabelle , um die Kapazitätsmatrix zu finden. EMS-Lösung für die Gesamtkapazität ist F (Abbildung 3) und es stimmt sehr gut mit dem theoretischen Ergebnis überein.

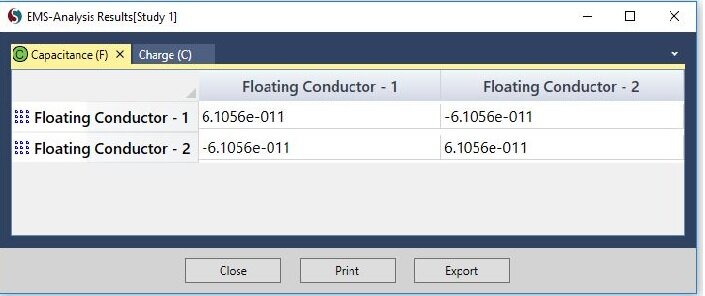
Abbildung 3 - EMS-Ergebnisse für die Kapazität