Capacitance Calculation for Parallel Plate Capacitors

What is a capacitor?

A capacitor stores electrical energy differently from batteries. It redistributes electrons without producing them. When connected to a battery, it charges and stores energy for use. A basic capacitor, like a parallel plate capacitor, consists of two metal plates separated by a gap with an insulator, typically air, in between.

. 

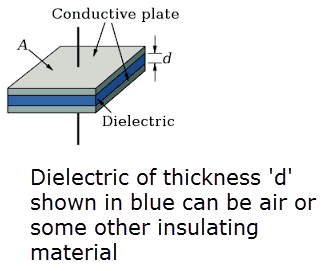
Figure 1 - Parallel plate capacitor

How does a capacitor store charges?

In Figure 1, connecting the top plate to the battery's positive terminal and the bottom plate to the negative terminal charges the capacitor. Electrons move, creating positive and negative charges on the plates. This makes a brief light bulb glow when connected, but it turns off when the plates regain neutrality.

How are capacitors measured?

Capacitors are rated by their capacitance, measured in Farads or Microfarads. More capacitance means the capacitor can store more charge.

What role does the dielectric play?

The dielectric in a capacitor is crucial because it affects the electric field within it. As the capacitor charges, the electric field builds up in the dielectric. However, if the electric field becomes too strong, the dielectric can break down and turn into a conductor, rendering the capacitor unable to store charge.

Our example – a capacitor with multiple dielectric

Let's consider a scenario with multiple dielectrics in a capacitor, as depicted in Figure 2. Our goal is to calculate the capacitance of this capacitor using EMS.

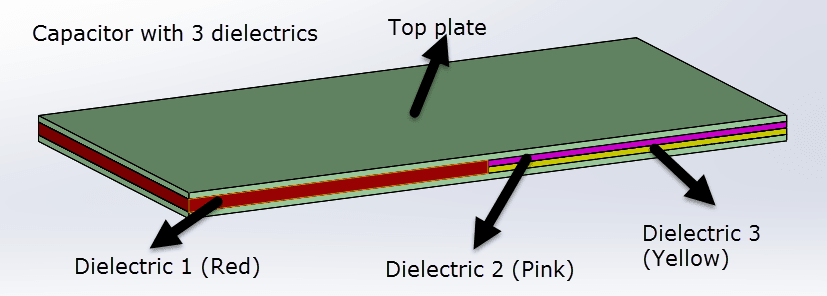
Figure 2 - Capacitor with 3 dielectrics

EMS has the capability to:

Capacitance calculation EMS results

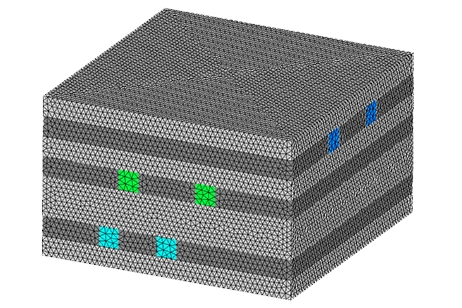
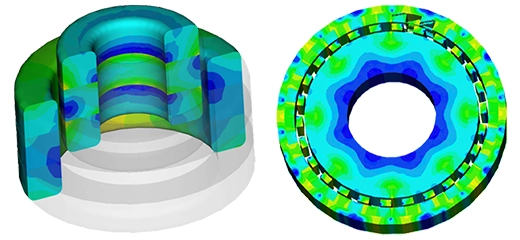
According to EMS, the capacitance value is 6e-11 Farads, as shown in Figure 3. Additionally, Figure 4 displays the electric field distribution in the dielectric region when the capacitor is connected to a 12 V battery.

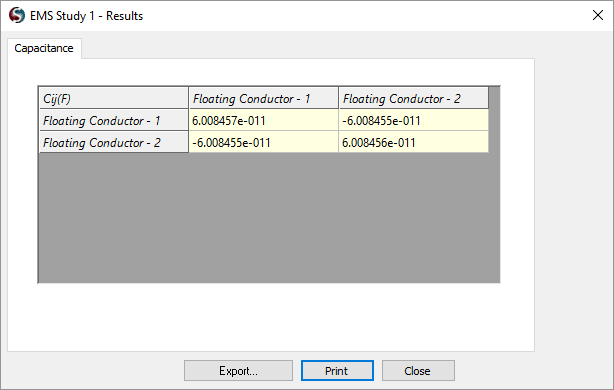
Figure 3 - Capacitance as computed by EMS

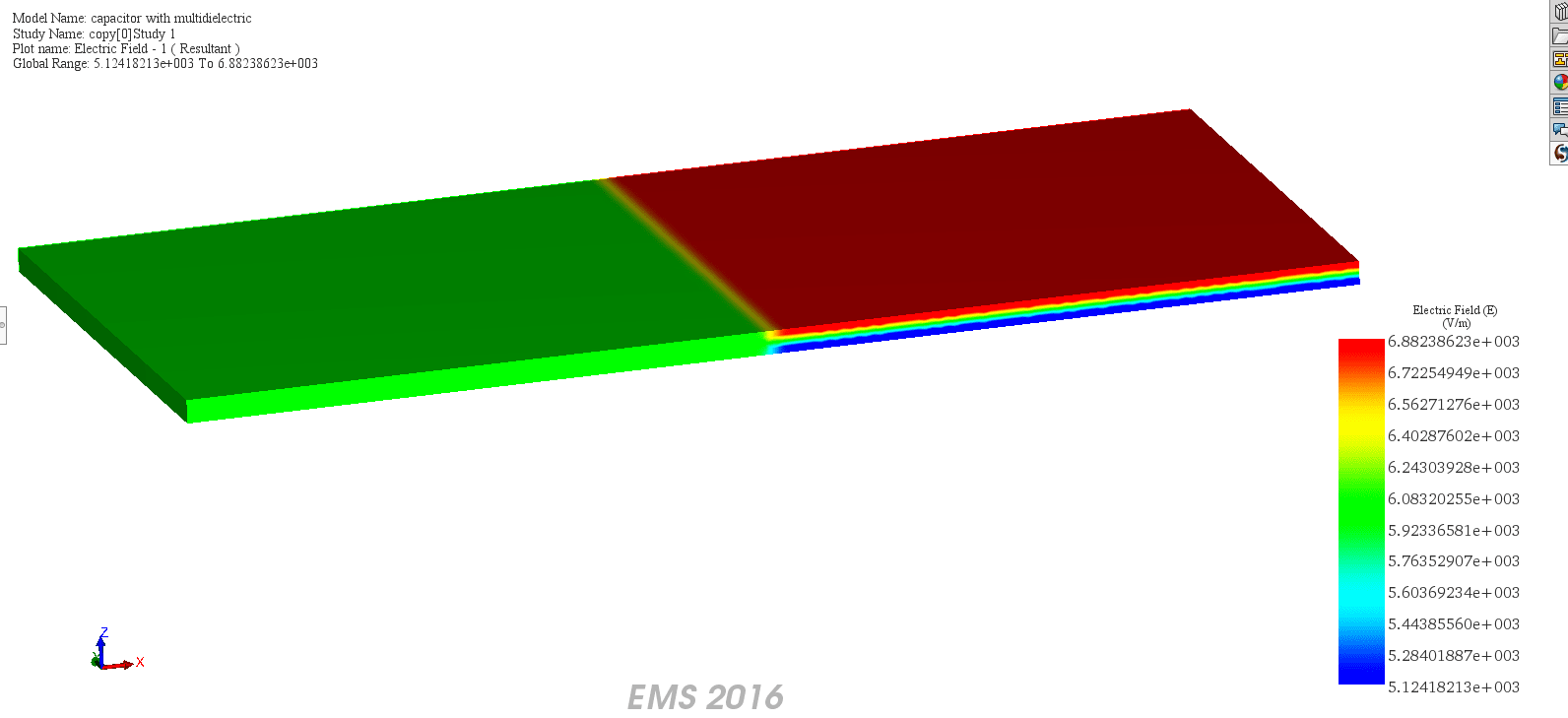
Figure 4 - Electric field distribution in the dielectirc

Validation

The formula for the theoretical result is derived from the source mentioned below.

Conclusion

This application note elucidates the fundamentals of capacitors, their mechanism for storing charge, and the crucial role of the dielectric material. It differentiates capacitors from batteries by highlighting their ability to redistribute electrons rather than produce them, thus storing electrical energy for immediate use. The note further delves into how capacitors are measured in terms of capacitance, with higher capacitance indicating a greater charge storage capacity. A significant focus is placed on the dielectric's function, emphasizing its importance in maintaining the capacitor's ability to store charge without succumbing to breakdown under strong electric fields.

An example featuring a capacitor with three different dielectrics is presented to demonstrate EMS software's capability to calculate capacitance accurately. EMS not only computes the capacitance, which aligns closely with theoretical results but also visualizes the electric field distribution within the dielectric, thereby assessing the risk of dielectric breakdown. This application note showcases the practical application of EMS in evaluating capacitor designs, ensuring their reliability and effectiveness in various electrical circuits and systems.

References

MIT OpenCourseWare - http://ocw.mit.edu (8.02SC Physics II: Electricity and Magnetism, Fall 2010)