振動は、ほとんどの機械システムが直面する主要な問題です。この有害な動作を軽減するために、さまざまな減衰方法が発明されています。これらの中で、磁歪材料に基づくアクティブ振動制御の場合のように、スマート材料を使用して振動量を減少させています。スマート材料は、温度、電圧、磁場などの信号に応答して生成します。磁気粘性流体、形状記憶合金、磁歪材料などの材料は、ある種類のエネルギーを別の種類のエネルギーに変換する能力を備えています。したがって、それらを使用すると、デバイスの全体的なパフォーマンスが向上します。
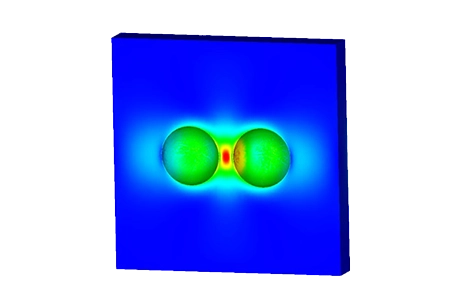
磁歪は、外部磁場の影響により材料の形状が変化する現象です。磁歪の原因は、小さな磁区の回転による長さの変化です。構造の内部歪みは、この配向と再配向によって引き起こされます。磁歪が正の場合、構造内のひずみにより、磁場の方向に材料が伸びます。延伸の過程で、断面積は減少しますが、体積はほぼ一定に保たれます。検出されたボリュームの変化は小さすぎるため、通常の動作条件下では無視できます。磁場がより重要になると、より多くのドメインが磁場の同じ方向に整列します。このプロセスは、すべての磁区が磁場と整列する飽和点に達するまで続きます。
EMS は、磁気機械場間の結合機能により、マルチフィジカル シミュレーションを保証します。この例では、 EMS は、2 つの異なる領域で、2 つの異なる電流密度の下で、線形および高度に飽和した磁性材料であるケイ素鋼 RM50の形状に対する定常磁場の影響を確認するのに役立ちます。
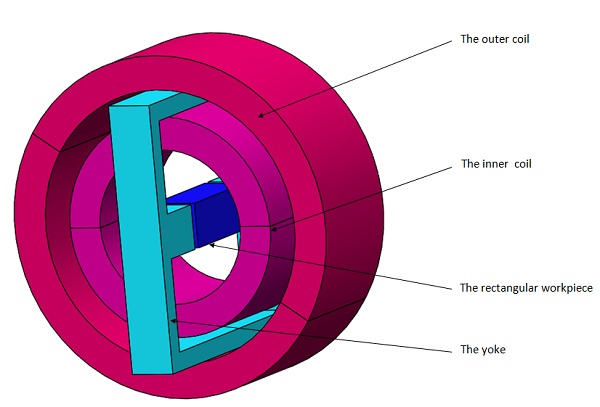
問題の磁気システムを下の図に示します。これは、定電流が供給される 2 つの同心に巻かれたコイルで構成されています。このシステムには、強磁性ヨークで囲まれた長方形の試験体も含まれています。
現在のモデルは、ヨークと試験体に割り当てられた強磁性材料の線形領域と飽和領域での長方形の試験体の機械的変形を見つけることを目的としています。ボディの変形をテストするために、2 つの異なる電流密度が使用されています。
EMSで構造解析と組み合わせた静磁スタディを作成した後、次の 4 つの重要な手順を常に実行する必要があります。
以下の表1は、使用された材料の特性です。電磁気方程式は、完全な解領域で解かれます。応力解析は、長方形のワークピースでのみ実行されます。
表 1 -材料特性
材料 | 比透磁率 | 電気伝導度 (Mho/m) | 弾性率 (Pa) | ポアソン比 |
銅 | 1 | 5.9980e+07 | 不要 | 不要 |
空気 | 1 | 0 | 不要 | 不要 |
ケイ素鋼（RM50） | * 2175 (リニアケース) | 2.1186e+06 | 2.035e+011 | 0.285 |
図2に珪素鋼材(RM50)のBH曲線を示します。
図 2 -ケイ素鋼 (RM50) の BH 曲線この研究では、問題の電流源として 2 つの巻線コイルが定義されています。
表 2 -コイル情報
ターン数 | 線径（mm） | 電流振幅 (A) | ||
Wound Coil 1 | 1 | 0.91168568mm | ケース 1 の場合は 47336.25 | |
Wound Coil 2 | 1 | 0.91168568mm | ケース 1 の場合は 4887.5 | |
長方形のワークピースの 4 つのエッジに対する固定拘束 (下の図 3 で強調表示)
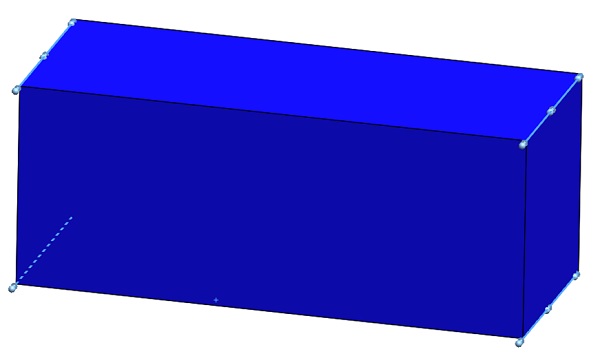
図 3 -モデル エッジに適用された固定拘束
メッシングは、設計解析において非常に重要なステップです。 EMS は、モデルの体積、表面積、およびその他の幾何学的詳細を考慮して、モデルの全体的な要素サイズを推定します。生成されるメッシュのサイズ (節点と要素の数) は、モデルのジオメトリと寸法、要素サイズ、メッシュ許容値、およびメッシュ コントロールによって異なります。おおよその結果で十分な設計解析の初期段階では、解析を高速化するために、より大きな要素サイズを指定できます。より正確な解を得るには、より小さい要素サイズが必要になる場合があります。
図 4 -メッシュ モデル
図 5 は、試験体とヨークが非線形透磁率を示し、2 番目の印加電流下にある場合の磁気システム全体の磁束の 3D プロットを示しています。
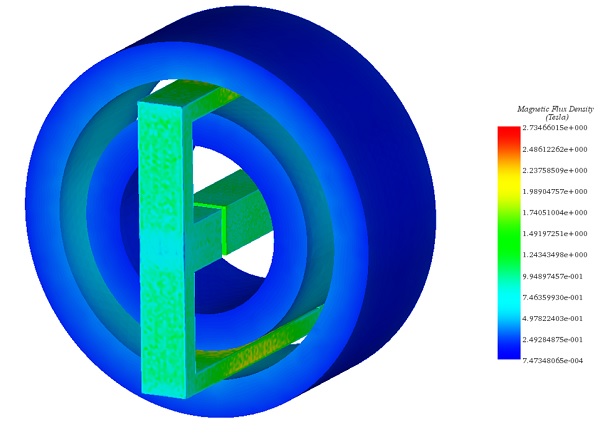
図 5 -磁束プロット
図 6 は、2 番目に処理された電流密度のケースについて、2 つのコイルの電流密度分布を示しています。
図 6 -電流密度プロット
図 7 は、ヨークと試験体の透磁率が非線形である場合に、2 番目に印加された電流密度の下での長方形の 3D 試験体の機械的変形を示しています。
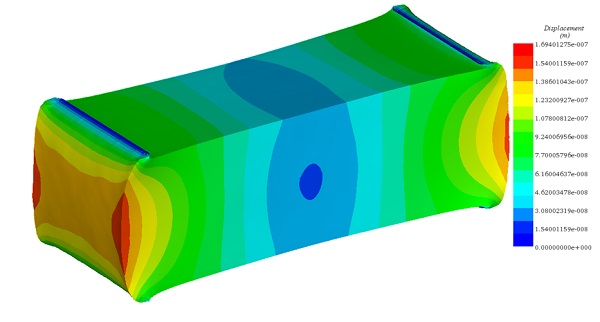
図 7 -結果の変位プロット
表 3 - 2 つの異なる透磁率を使用した、2 つの使用電流密度下でのワークピースのたわみ
電流密度 | 線形透磁率 | 非線形透磁率 |
| J=2.5e+06 A/m^2 | 0.98 | 0.88 |
| J=25e+06 A/m^2 | 87.94 | 5.65 |
EMS は、線形領域と飽和領域の両方で、磁場の影響下での磁性材料の変形を研究する可能性を提供します。さまざまな動作条件下で、非線形透磁率を持つ磁性材料などの現実的な材料特性の機械的挙動をシミュレートできます。
[1]:Se-Hee Lee, Xiaowei He, Do Kyung Kim, Shihab Elborai, Hong-Soon Choi, II-Han Park and Markus Zhan.2005. Evaluation of the mechanical deformation in incompressible linear and nonlinear magnetic materials using various electromagnetic force density methods. Journal of applied physics. Volume 97, Issue 10.
| Share on |
English (CA)
Deutsch
日本語