薄膜抵抗器
薄膜抵抗器は、絶縁基板上に均一な金属薄膜を真空蒸着したものです。電子の流れがスムーズで、抵抗の温度係数が小さく、高精度応用に適しています。

図1 -薄膜抵抗器
薄膜抵抗モデル
この例では、 EMSとSOLIDOWRKS を使用して、薄膜抵抗のモデル化と解析を行います。図 2 と 3 は、解析された抵抗器の構造パラメーターと 3D モデルを示しています。

図 2 -モデルの寸法
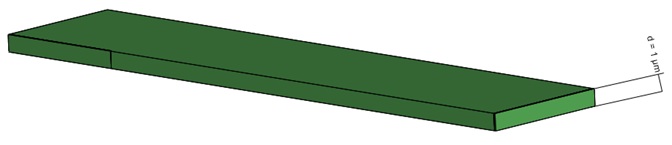
図 3 -薄膜抵抗の 3D モデル
EMSで電気伝導解析
電気伝導モジュールは、主に電圧差による導体の電流の流れを計算するために使用されます。このモジュールによって生成される結果は、静電ポテンシャル、静電界、電流密度、絶縁破壊電圧、抵抗です。電気伝導モジュールは、熱および運動解析と結合する機能を備えており、幅広い問題の解決に役立ち、いくつかの応用で使用できます。
この例では、電気伝導モジュールを使用して EMS 内部の抵抗を計算します。抵抗は、電圧と電流の比として 2 点間で定義されます。したがって、ユーザーは抵抗セットの入口ポートと出口ポートを指定する必要があります。入口ポートは電流が抵抗に流れ込む場所であり、出口ポートは電流が出る場所です。 EMS は、入口ポートと出口ポートの間の電圧差と、抵抗器セットを流れる電流を自動的に計算します。電流と電圧から、抵抗が推定されます。
解析設計
EMSで電気伝導解析を実行するには、これらの 4 つの手順に従う必要があります。
新しい電気伝導スタディを作成します
パーツに適切な材料を適用する
適切な荷重と拘束を加える
- メッシュを作成して解析を実行する
材料
この場合、薄膜抵抗は、2e+7 S/m の導電率を持つ金属材料でできています。
負荷・拘束
下の図は、固定電圧が適用される面を示しています。それらの値は、左側が 0.001V、右側が -0.001 です。抵抗セットは同じ面にも適用されます。

図 4 -固定電圧と抵抗が適用される面のハイライト
メッシュ
メッシュは、すべてのFEM解析にとって重要です。結果の精度と解析時間は、メッシュサイズに大きく依存します。細かいメッシュ (要素サイズが小さい) のモデルでは、非常に正確な結果が得られますが、計算時間が長くなります。モデルの全体的なサイズを推定した後、 EMSによってメッシュを自動的に生成できます。また、EMS では、メッシュ調節によって固体と表面のメッシュサイズを調整できるため、メッシュ作成の柔軟性がさらに高まります。この例では、固定電圧が適用される面が細かくメッシュ化されており、要素の最大寸法は 0.1 um です。モデル全体の最大要素サイズは 0.3 um です。図 5 に最終的なメッシュを示します。
EMSによって計算されたFEM結果
スタディを実行した後。上記の結果はEMSによって生成されます。より正確な結果を得るために、アドバンスドスタディプロパティの標準精度のオプションが高精度に変更されました。高精度オプションでは、解析に時間がかかりますが、より正確な結果が得られます。
解析された薄膜抵抗の抵抗値は、以下の式で計算できます [1]。
図 6 は、 EMSで有限要素法によって計算された抵抗値を示しています。理論上の結果とEMSの結果はほぼ同じです。図 7 と 8 は、それぞれ電流密度と静電ポテンシャルの 3D プロットを示しています。
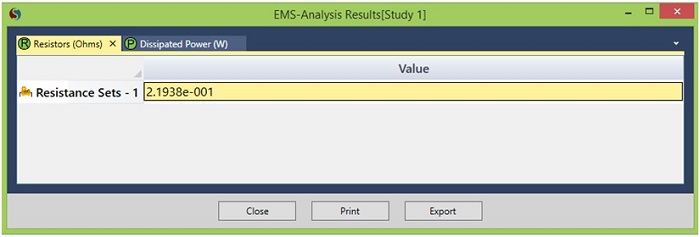
図 6 - EMS によって計算された抵抗
図 7 -電流密度、ベクトル プロット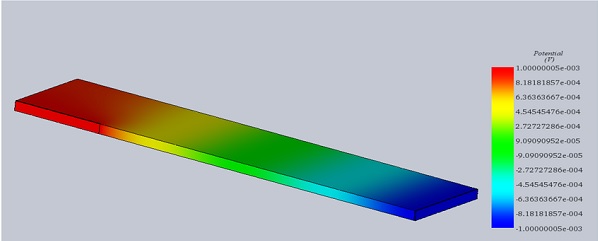
図 8 -ポテンシャル プロット
結論
薄膜抵抗の分析結果は、 EMS .EMWorks の低周波パッケージEMS と非常によく一致します。EMWorks の低周波パッケージ EMSは、3D CAD ソフトウェア (Solidworks、Autodesk Inventor、SpaceClaim) に完全に統合されており、エンジニアが製品を最適化し、時間とお金を節約するのに役立ちます。
参考文献
[1]: Conformal Mapping: Methods and Applications, Roland Schinzinger, Patricio A. A. Laura, 1991, Elsevier Science Publishers, B.V., p. 224. ISBN 0-486-43236-X (pbk).



