序章
渦電流カプラーは、渦電流の原理に基づいて動作する非接触結合システムであり、近くの変化する磁場によって導体内に循環電流が誘導されます。この誘導電流は、磁場源 (巻線または PM によって作成される) に対抗する磁場を作成します。電気モーターおよび発電機では、渦電流は望ましくなく、可能な限り低減することを目的としています。しかし、これは渦電流ベースのカプラには当てはまりません。導体とソース (PM アレイ) の間で生成された力により、導体は PM ソースの動きに追従できます。これらの力により、2 つの回転機械システム間のトルク伝達が、具体的な接触なしで確実に行われます。
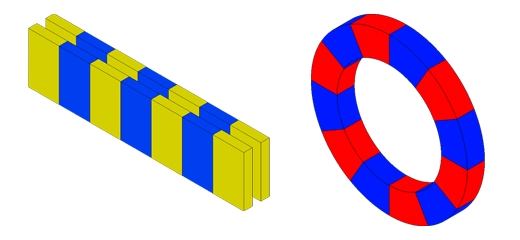
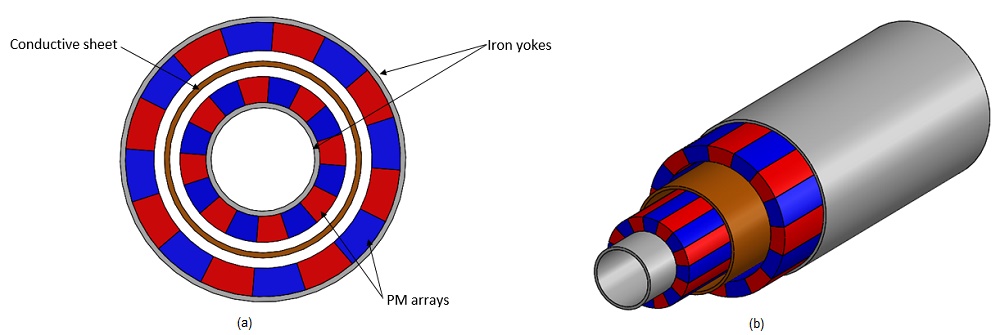
本論文では、両面永久磁石 (DSPM) 構成の場合のラジアル型渦電流カプラーを検討します。図 1 は、DSPM カプラーの実際のプロトタイプと幾何学的設計を示しています。これは、2 つの同心円状の放射状に分極された PM 配置で構成され、磁化の方向が交互になっています。内側と外側の鉄ヨークが PM 配列を支えており、その間に導体の円筒形シートが配置されています。

| 材料 | 透磁率 | 電気伝導性 (S/m) | 残存 保磁力 |
| 鉄 | 4000 | 10 | - |
PM-NdFeB | 0.823 | 0 | 1.4T 1353000A/m |
| Stainless Steel 304 | 1 | 1.37E+6 | - |
結果
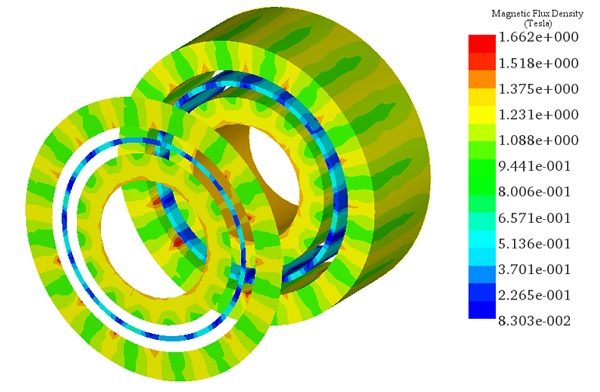
(a)
(ロ)
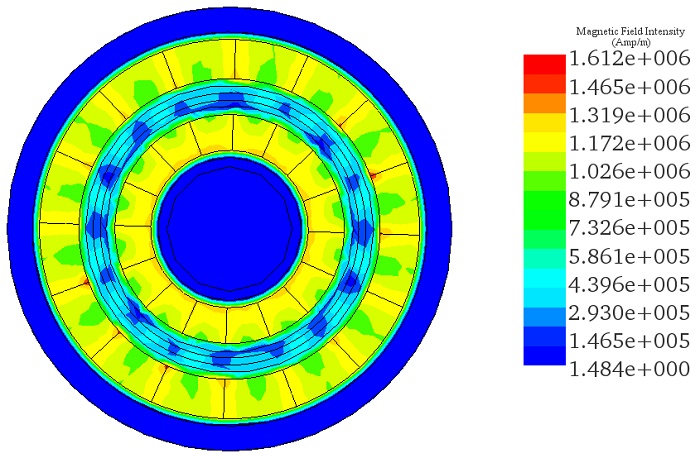
速度が一定であるため、図 5 のアニメーションに示すように、シミュレーション時間中、渦電流は比較的変化しません。
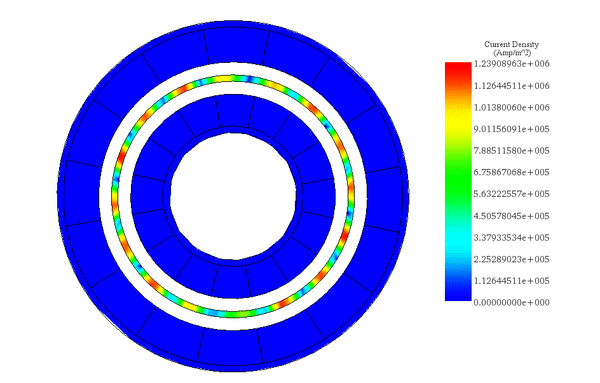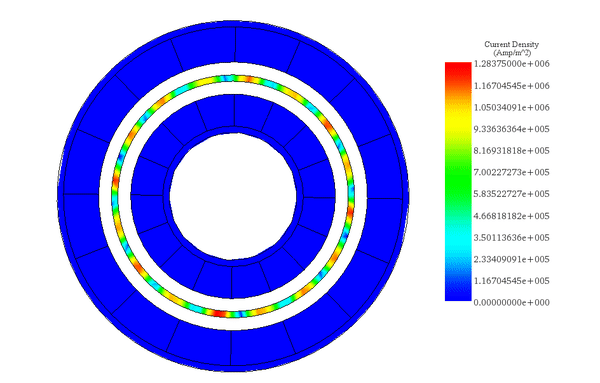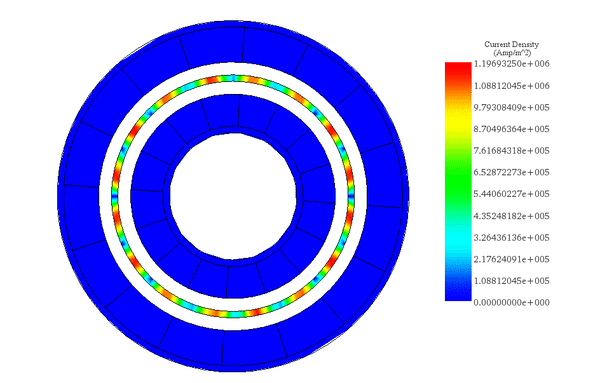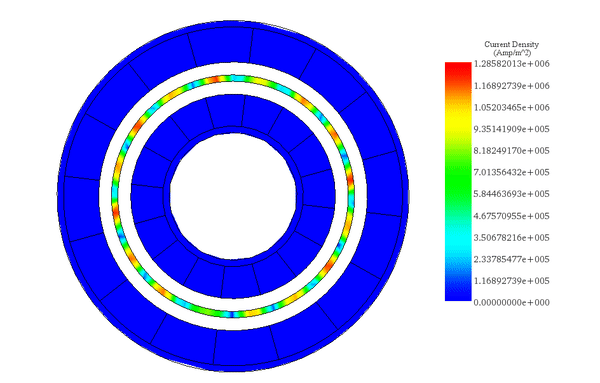
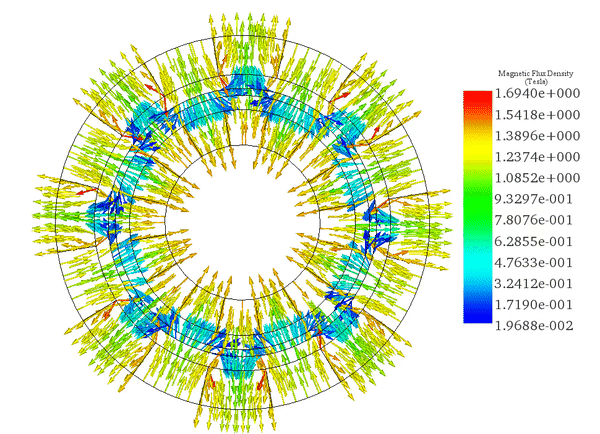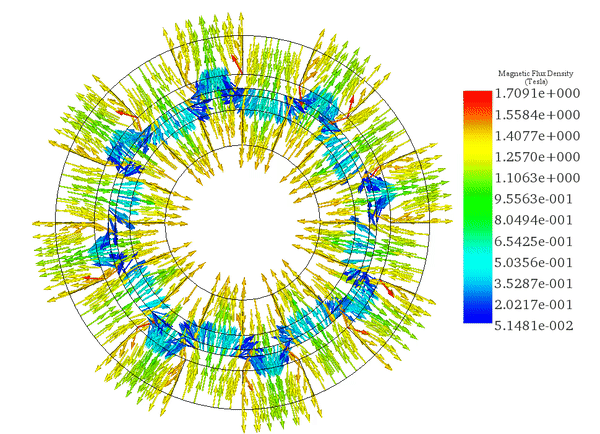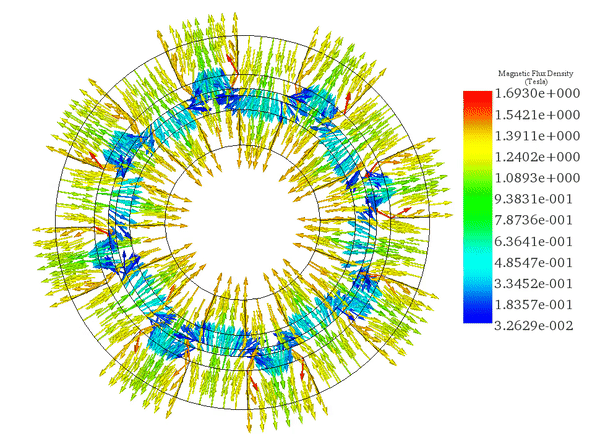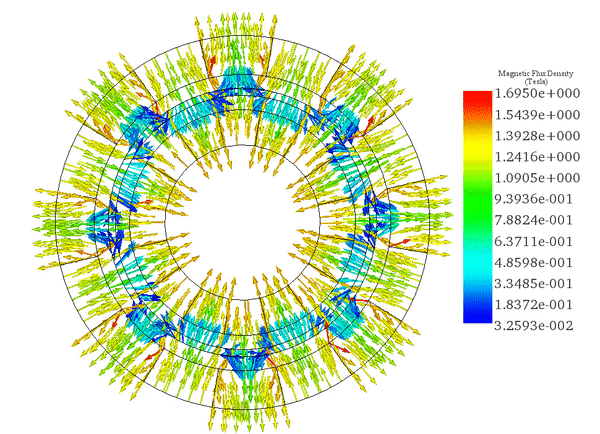
(a)
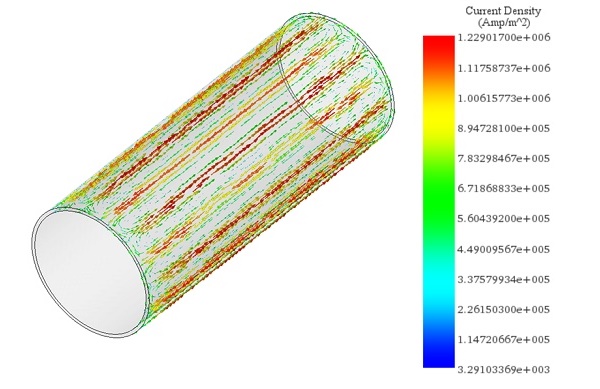
(a)
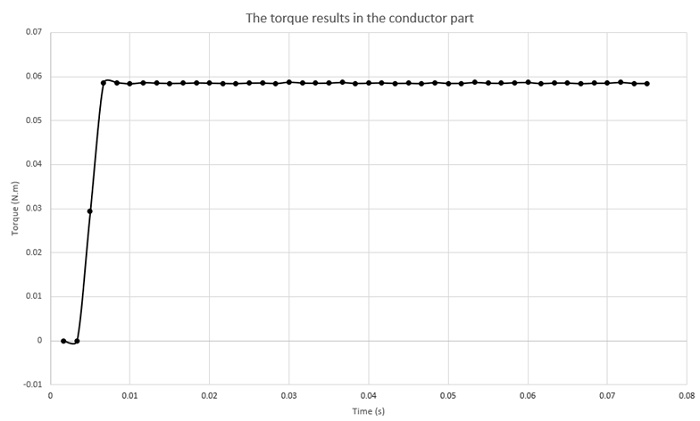
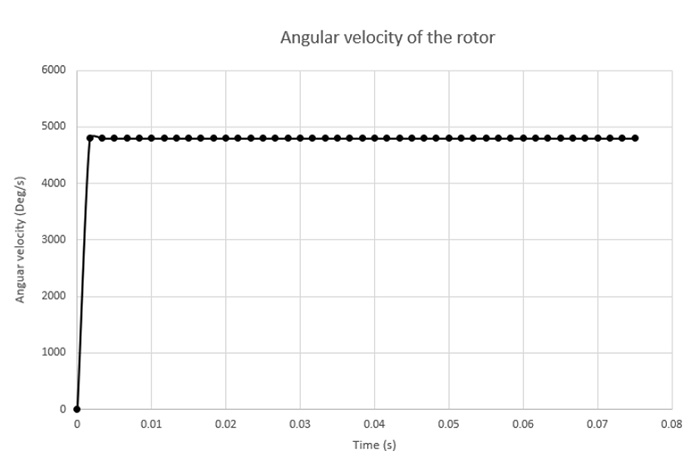
(ロ)
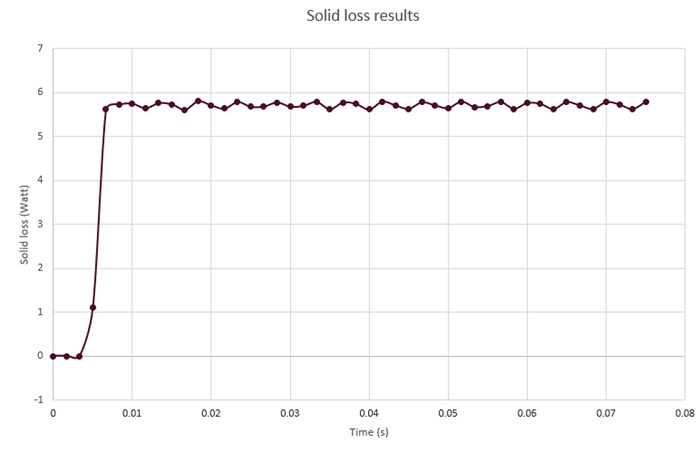
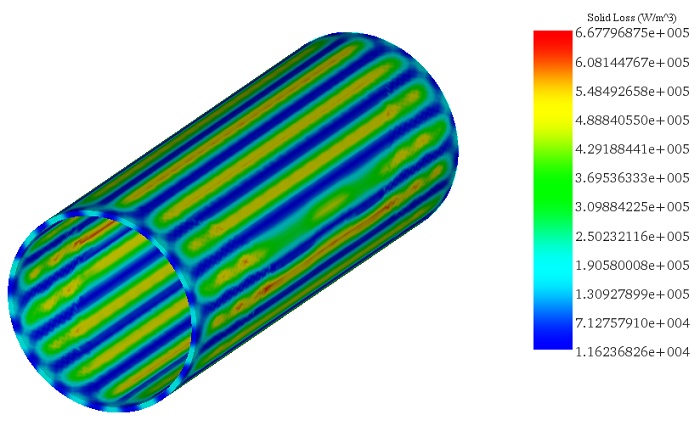
結論
この検討を通じて、EMSツールは、定常状態条件下でのラジアル磁束渦電流PMカプラーの磁束密度分布、誘導電流、渦損失、および生成されたトルクを予測することを可能にしました。得られた結果は、参考で検討された 3D 分析分析の検証に役立ちました [2]。誘導損失の推定により、EMS ツールに基づく今後の作業で、そのようなデバイスの熱挙動を実行できるようになります。
参考文献
[1]. Erasmus, Abraham Stephanus. Analytical modelling and design optimization of the Eddy Current Slip Coupler. Diss. Stellenbosch: Stellenbosch University, 2017.
[2] . Zhu, Zina, and Zhuo Meng. "3D analysis of eddy current loss in the permanent magnet coupling." Review of Scientific Instruments 87.7 (2016): 074701.